双重差分模型

原视频传送门

1、双重差分模型(DID)的介绍

双重差分法通常被用来分析某处理行为的效应，该行为常表示为一个 0-1 变量。双重差分法对数据有三个要求：

• 需采用观测数据(observational data)，而非实验数据(experimental data)。双重差分实则是通过两次差分来优化观测数据来模拟实验数据；
• 需要包含处理组个体和非处理组个体；
• 既有处理行为发生前的数据，也有处理行为发生后的数据；

双重差分法又可以分为传统双重差分法和多期双重差分法等。

2、传统双重差分法

当处理行为发生在一个时间点，我们就称采用的方法为传统双重差分法，也叫经典双重差分法、两期双重差分法。比如下表的数据：

	处理组		非处理组（对照组）
处理前	A		B
处理后	C		D

如果我们单独对比 A、C 或者比较 C、D，显然都有明显的因素没有考虑而不科学。一种方法是使用倾向得分匹配，这种方法会尽量找到一个 使得 B 与 A 相似的数据作为对照组进而减小两组本身差异对分析的影响，从而实现只比较 C、D 即可。但现实生活中这种相似度高的数据是极难找到的，这种情况下我们就会使用双重差分法。

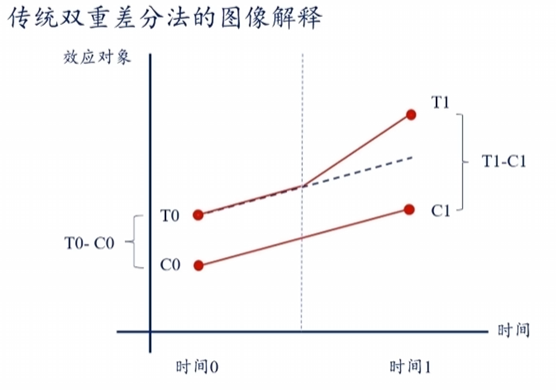
在多重差分法中，\(C-D=处理行为效果+两组个体差异\)，\(A-B=两组个体差异\)，这是第一重差分，而二者相减就会得到处理行为的效果，这就是第二重差分。另外，这两次差分的顺序是可以改变的，即\(C-A=处理行为效果+时间因素影响\)，\(D-B=时间因素影响\)。

3、回归模型中的双重差分法

\(回归模型：Y_{it}=\beta_0 + \beta_1 \times T + \beta_2 \times D + \beta_3 \times D \times T + \epsilon \)

其中：

• \(Y_it\) 是因变量，处理行为的效用对象
• \(T\) 时间变量，0-1变量，表示处理行为发生前后
• \(D\) 处理组变量，0-1变量，表示是否经过处理
• \(D \times T\) 交互项，该项只有在处理行为发生后且经过处理时取1，其余都取0，其系数即为所求的“处理行为的效果”

用回归的好处在于可以添加控制变量，考虑除了时间和处理以外其他可能导致变化的影响因素。影响\(Y_it\)的非时间控制变量可以直接加入，注意多重共线性即可；而时间控制变量酌情添加，添加方法一是直接把控制变量\(T\)进行展开成一组0-1变量，二是在一的基础上把交乘项中的\(T\)也进行展开，替换为一组0-1时间变量，但方法二中\(D\)与那组时间变量存在多重共线性，常用的解决方法是删掉处理行为发生的那个时间点对应的变量。同时要注意的是在处理行为发生前时间变量的系数应该是经济和统计意义都不显著，下图中为\(\beta_3\)和\(\beta_4\)，即绝对值趋向于0。

4、多期双重差分法

当处理行为发生在不同时间点，我们称其为多期双重差分法，也叫多时点双重差分法、渐进双重差分法。