数据结构——树遍历和图形

Tree Traversals

遍历一棵树有一些自然的方式：

• Level order traversal. Breadth First Search(BFS)，广度优先搜索
• Depth-First traversal(DFS)，深度优先搜索，又可分为三种：pre-order, in-order and post-order.

以下面这棵树为例：

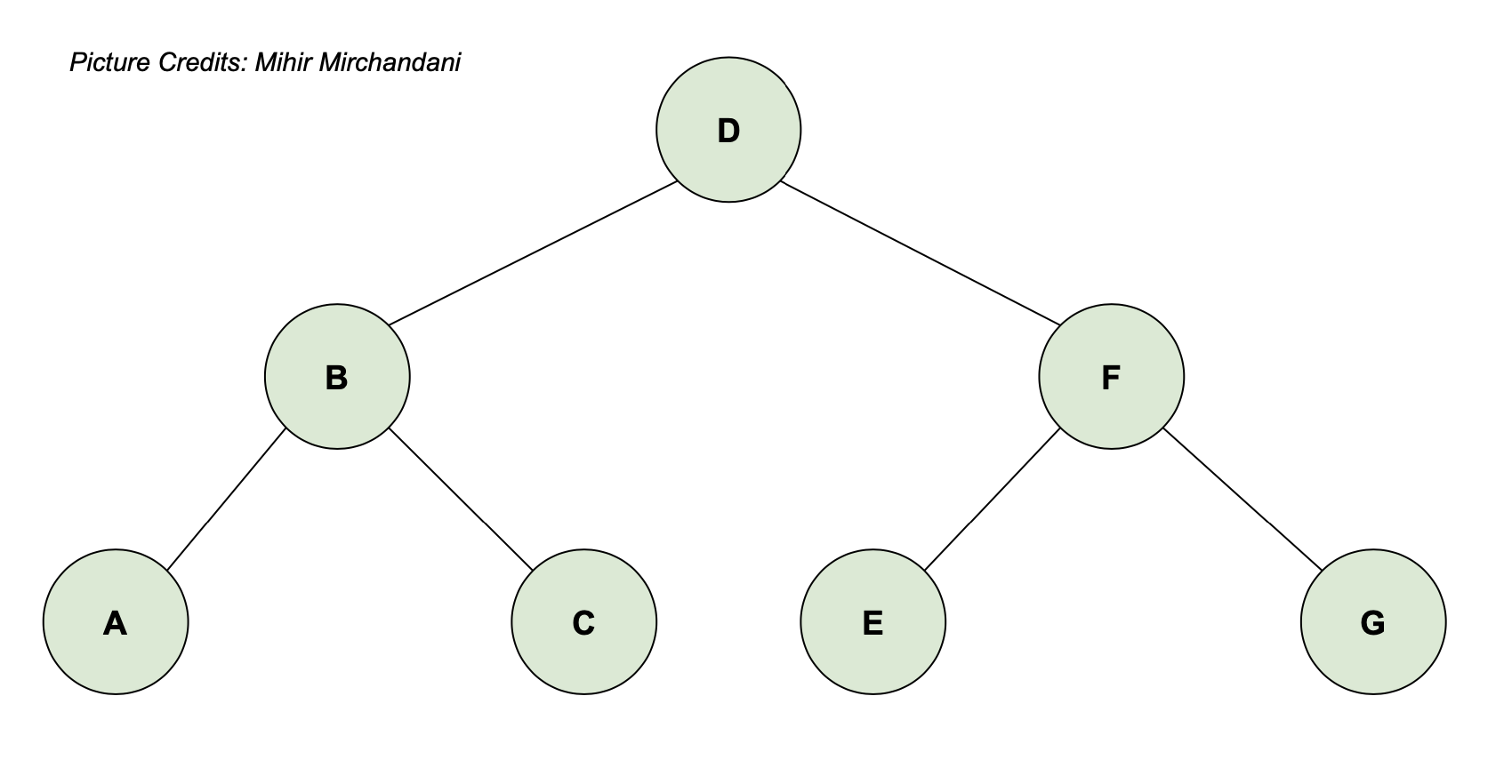
我们给出该树的基本结构：

public class BST<Key> {
    private Key key;
    private BST left;
    private BST right;

    public BST(Key key, BST<Key> left, BST<Key> right) {
        this.key = key;
        this.left = left;
        this.right = right;
    }

    public BST(Key key) {
        this.key = key;
    }

    public static void main(String[] args) {
        BST<Integer> root = new BST<>(D);
        root.left = new BST<>(B);
        root.right = new BST<>(F);
        root.left.left = new BST<>(A);
        root.left.right = new BST<>(C);
        root.right.left = new BST<>(E);
        root.right.right = new BST<>(G);
    }
}

Level Order Traversal

按照级别从左到右遍历，顺序为D -> B -> F -> A -> C -> E -> G。

    private void printLevel(BST<Key> node, int level) {
        if (node == null) return;
        if (level == 1) {
            System.out.print(node.key + " ");
        } else {
            printLevel(node.left, level - 1);
            printLevel(node.right, level - 1);
        }
    }

    public void levelOrderTraversal() {
        int height = height(this);
        for (int i = 1; i <= height; i++) {
            printLevel(this, i);
        }
    }

    private int height(BST<Key> node) {
        if (node == null) return 0;
        return 1 + Math.max(height(node.left), height(node.right));
    }

Pre-Order Traversal

这是先序遍历，顺序是：访问根节点 -> 递归访问左子树 -> 递归访问右子树。

    public void preOrderTraversal() {
        System.out.print(key + " ");

        if (left != null) {
            left.preOrderTraversal();
        }

        if (right != null) {
            right.preOrderTraversal();
        }
    }

In-Order Traversal

这是中序遍历，实现顺序是：递归访问左子树 -> 访问根节点 -> 递归访问右子树。

    public void inOrderTraversal() {
        if (left != null) {
            left.inOrderTraversal();
        }

        System.out.print(key + " ");

        if (right != null) {
            right.inOrderTraversal();
        }
    }

Post-Order Traversal

这是后序遍历，顺序是：左子树 -> 右子树 -> 根节点

    public void inOrderTraversal() {
        if (left != null) {
            left.inOrderTraversal();
        }

        if (right != null) {
            right.inOrderTraversal();
        }

        System.out.print(key + " ");
    }