Zhang Zhuhe

Hello, I’m an ungraduated student of Tongji University

2 分钟阅读

详细介绍见 Josh Hug 为 Berkeley CS61B 编写的教材

最新版本

一个数据结构可视化网站

Binary Search Trees

为了改进搜索性能，我们可以使用二叉搜索，最基础的改进是引用中间节点，然后翻转节点指针遍历两边；同样，我们可以这样向每个递归半部分的中间添加指针以进一步优化，这样就形成了二叉树，每个节点都一分为二。

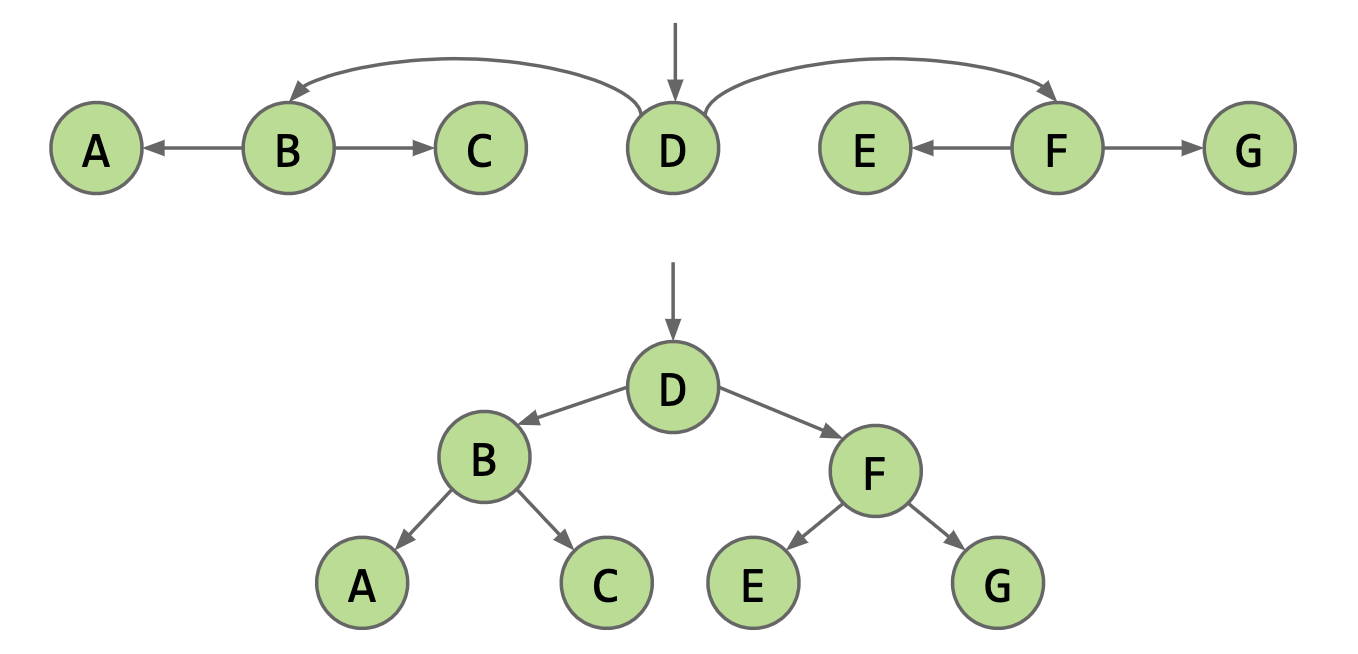
BTS 二叉搜索树：除了需要满足二叉树的定义，对树中的每个节点还需满足：

  • 节点 X 左侧子树中的每个节点的值都小于 X 的值；
  • 节点 X 右侧子树中的每个节点的值都大于 X 的值。

基础的 BST 模块如下：

private class BST<Key> {
    private Key key;
    private BST left;
    private BST right;

    public BST(Key key, BST left, BST Right) {
        this.key = key;
        this.left = left;
        this.right = right;
    }

    public BST(Key key) {
        this.key = key;
    }
}

接下来我将完成 BTS 模块中的一些操作。

find

find 操作的代码如下：

static BST find(BST T, Key sk) {
   if (T == null)
      return null;
   if (sk.equals(T.key))
      return T;
   else if (sk < T.key)
      return find(T.left, sk);
   else
      return find(T.right, sk);
}

insert

static BST insert(BST T, Key ik) {
  if (T == null)
    return new BST(ik);
  if (ik < T.key)
    T.left = insert(T.left, ik);
  else if (ik > T.key)
    T.right = insert(T.right, ik);
  return T;
}

delete

删除操作中，我们需要将情况分为三类：

  • 无子节点：直接删除其父指针即可；
  • 只有一个子节点：将父节点的子指针分配给节点的子节点即可；
  • 有两个子节点：我们选择一个新节点来替换需要删除的节点，新节点需要满足二叉搜索树的条件，可以用于替换的是左侧子树中的最大节点或右侧子树中的最小节点。这称为 Hibbard delete。

代码如下：

private static BTS findMin(BTS node) {
    while (node.left != null) {
        node = node.left;
    }
    return node;
}

static BTS delete(BTS T, Key dk) {
    if (T == null) {
        return null;
    }
    if (dk < T.key) {
        T.left = delete(T.left, dk);
    } else if (dk > T.key) {
        T.right = delete(T.right, dk);
    } else {
        if (T.left == null && T.right == null) {
            return null;
        } else if (T.left == null) {
            return T.right;
        } else if (T.right == null) {
            return T.left;
        } else {
            BTS successor = findMin(T.right);
            T.key = successor.key;
            T.right = delete(T.right, successor.key);
        }
    }
    return T;
}

Θ 与 O

\(Θ\) 符号表示算法的精确复杂度，它既提供了上界也提供了下界。换句话说，\(Θ(f(n))\) 表示存在常数 \(c_1、c_2 和 n_0\)，使得对于所有 \(n ≥ n_0\)，\(T(n)\) 满足 \(c_1 f(n) ≤ T(n) ≤ c_2 f(n)\)。也就是说，\(Θ\) 符号可以用来表示算法在输入规模增加时的行为是紧密围绕着一个函数的。

而大\(O\)符号用于描述算法的上界，即在最坏情况下算法的复杂度。比如，\(O(n)\) 表示在最坏情况下，算法的执行时间不会超过一个与输入规模 \(n\) 成正比的量。在数学上，\(O(f(n))\) 表示存在常数 \(c\) 和 \(n_0\)，使得对于所有 \(n ≥ n_0\)，算法的运行时间 \(T(n)\) 满足 \(T(n) ≤ c * f(n)\)。

B-Tree

对于树，Height 指最深的叶子的深度，而 depth 指与特定节点的根的距离，树的平均深度即为每个节点深度的平均值。

实际上，考虑随机的树，我们可以证明\(E(d)=2 \ln{n}\)并且\(E(h)=4.311 \ln{n}\)。

B-Tree Operations

为尽可能减少树的 height，我们的第一个想法是：在插入新值时不再插入新节点，而是将新值堆叠到适当位置的现有的叶节点中即可。但这种方法的问题在于，其又会导致大的叶节点几乎变成了一个值列表。

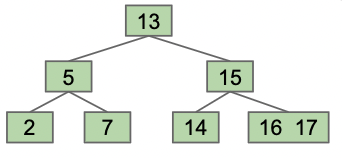
因此我们添加一个修复，当叶节点达到一定数量的值时，我们考虑向上移动一个值。

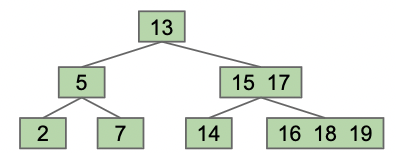
同时，向上移动后仍需满足二叉搜索的条件，因此我们需要第二个修复，把子节点进行分隔。

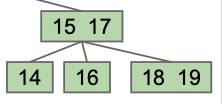
而如果根节点大于限制值，则我们被迫增加树的高度。

这样的树结构具有完美的平衡。如果根节点需要拆分，那么所有节点都将下推一级；而如果我们拆分叶或内部节点，则高度不会改变。 没有会导致不平衡的变化产生。

此结构就叫做 B-Tree，将每个节点限制为 3 个项目的 B-Tree 也称为 2-3-4 Tree 或 2-4 Tree（即一个节点可以有 2、3 或 4 个子节点）， 而将每个节点设置为两个项目限制则称为 2-3 Tree。

B-Tree 常用于具有大量记录的数据库与文件系统中。

B-Tree Invariants

B-Tree 有两个不变量

  • 所有叶子（最底层）与根的距离都相同；
  • 具有 k 个项的非叶节点必须恰好具有 k+1 个子节点。

Red Black Trees

Rotating Trees

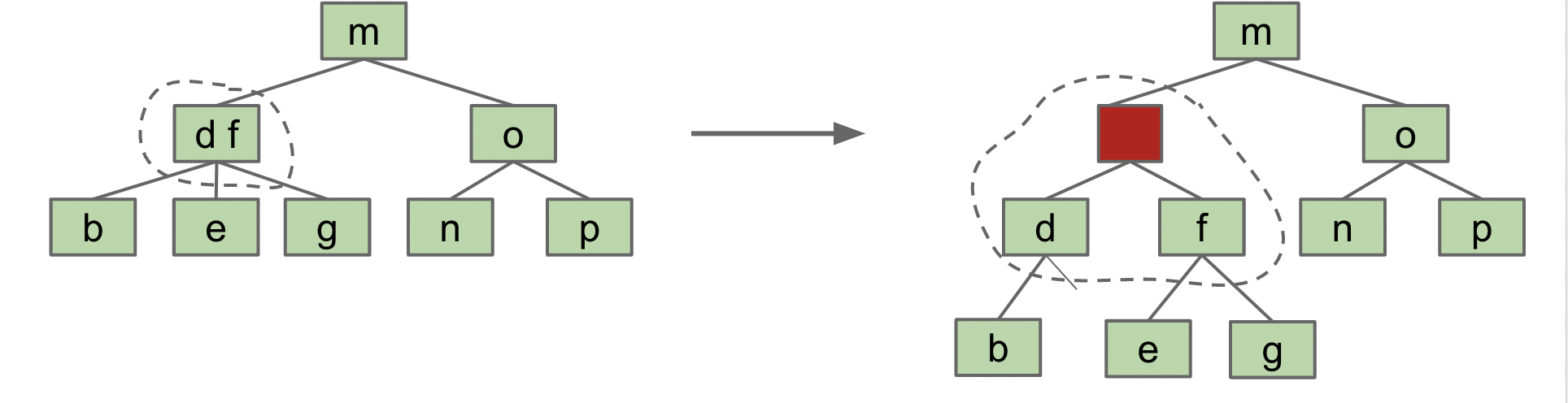
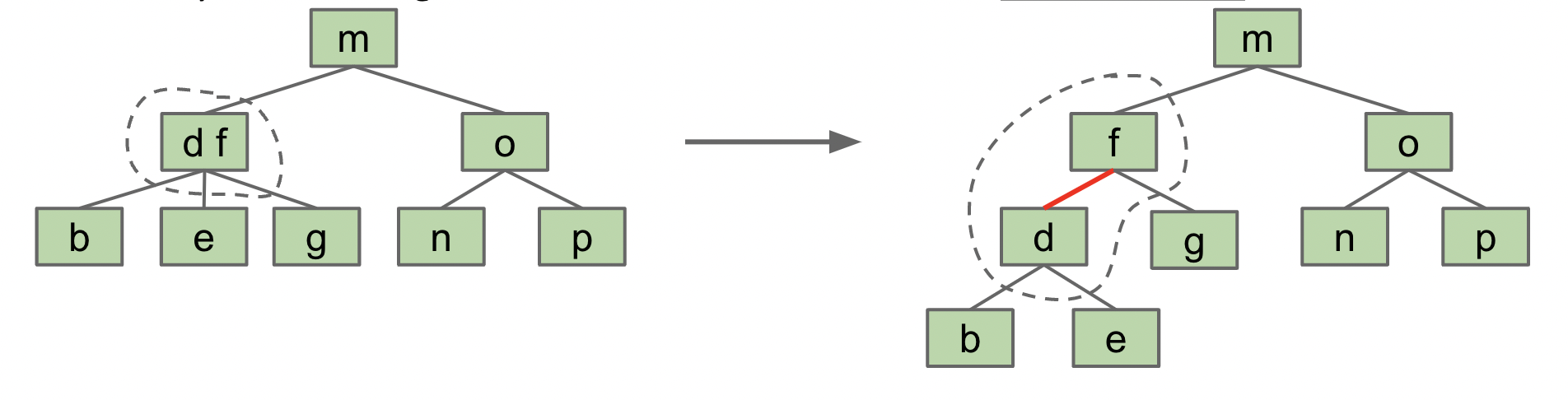
所谓旋转树，旋转的正式定义是：

  • rotateLeft(G): Let x be the right child of G. Make G the new left child of x.
  • rotateRight(G): Let x be the left child of G. Make G the new right child of x.

例如，将节点 G 向左旋转：

代码的实现如下：

private Node rotateRight(Node h) {
    // assert (h != null) && isRed(h.left);
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    return x;
}

// make a right-leaning link lean to the left
private Node rotateLeft(Node h) {
    // assert (h != null) && isRed(h.right);
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    return x;
}

旋转树的目的是对树的平衡性进行修复，不同的树的平衡性定义有所不同。

原文见OI wiki

Creating LLRB Trees

2-3 Tree 虽然具有很好的平衡性，但实现起来比较复杂；而 BST 虽然可能不平衡，但简单直观。我们希望把二者的优点结合，创建一个使用 BST 实现的树， 但结构上与 2-3 树一致，这就是 Red Black Trees 红黑树。

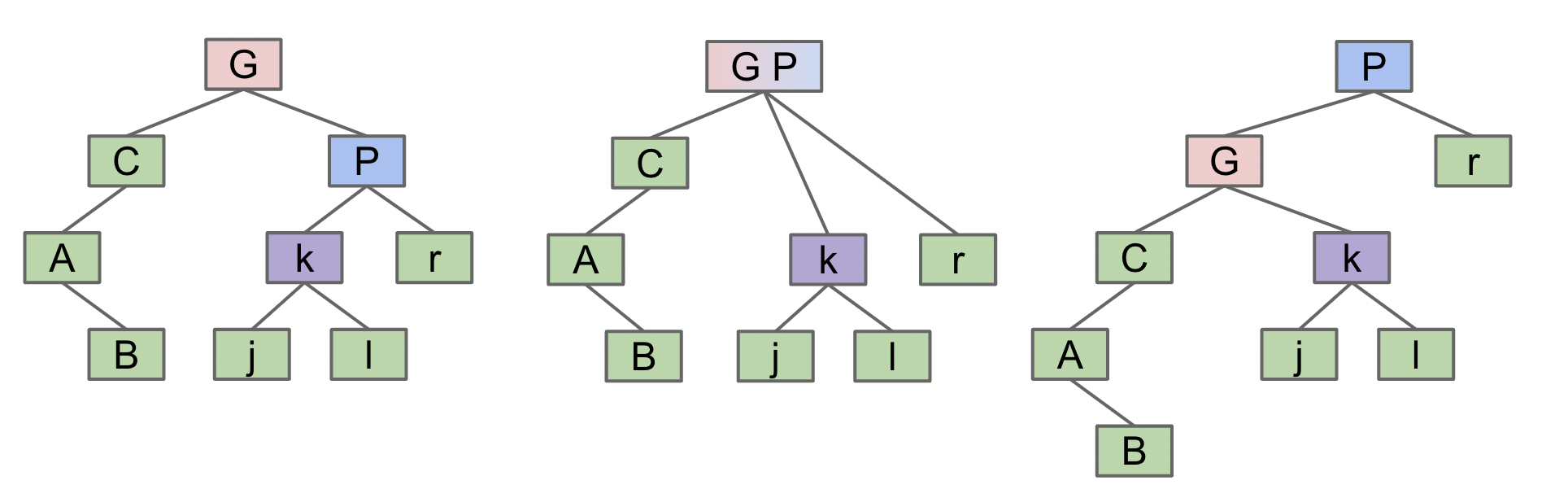
当 2-3 树中的内部节点只具有两个子节点时，我们不需要进行改动即同样是 BST 树。而当内部节点具有 3 个子节点时，我们可以创建一个虚拟的 Glue 节点， 用于显示其两个子节点实际上是该节点的一部分。如图：

但这样会占用更多空间，所以我们选择将虚拟的 Glue 节点转化为 Glue 链接，我们任意选择使左侧元素成为右侧元素的子元素，这样即会产生一个左倾的树。

图中红色的链接表示 Glue 链接，正常链接为黑色，这样的结构称为左倾红黑树(left-leaning red-black trees)。每棵左倾红黑树与 2-3 树都是一一对应的， 而 2-3-4 树与标准红黑树保持对应关系。

LLRB 树有以下特性：

  • 与 2-3 Tree 一一对应；
  • 没有节点有两个红色链接；
  • 没有红色的右链接；
  • 从 root 到 leaf 的每条路径都有相同数量的黑色链接
  • 高度不高于 2-3 Tree 的 2 倍加 1；
  • 红黑树的高度与条目数量（即树中所有独立的数据项的数量）的对数成正比。

Inserting LLRB Trees

LLRB 的插入总体与 BTS 一致，但为了保持结构，我们需要对一些情况进行旋转操作。

进行插入操作时，我们总是使用红色链接将新节点与其父节点连接，这是因为在 2-3 Tree 中，我们总是通过添加至叶节点来插入。有三种情况我们需要 额外操作维护 LLRB 的正确结构。

  • 情况 1：插入导致右倾

    • 操作：rotateLeft(node)
    • 左倾的红黑树永远不能有右红链接
    • 如果左侧子项也是红色链接，我们将暂时允许两个同时存在，以便在情况 3 中进行处理

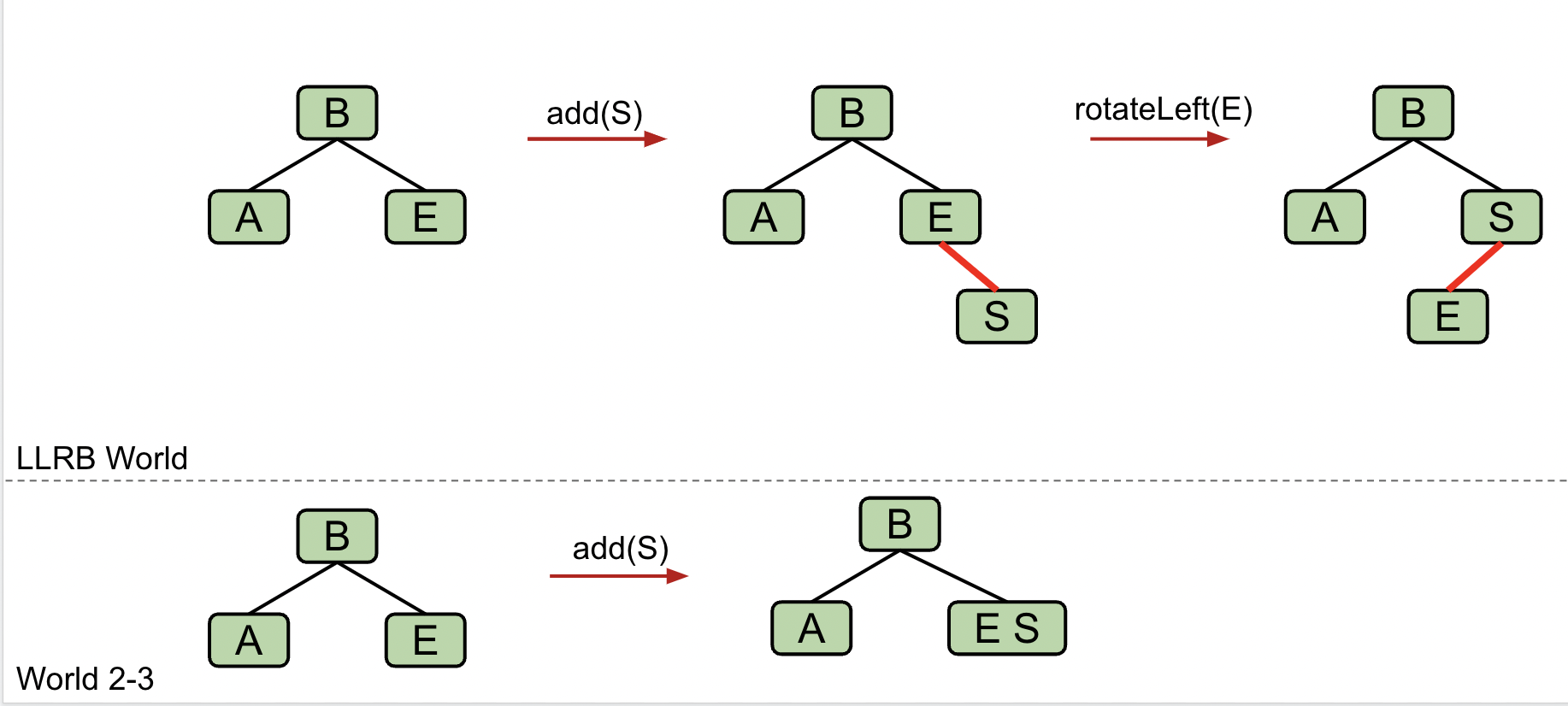
  • 情况 2：左侧有两个红色链接

    • 操作：rotateRight(node)
    • 左侧有两个红色链接导致我们有一个非法的四节点
    • 我们旋转生成一个与情况 1 中双红节点一样的结构，然后在情况 3 中进行处理

  • 情况 3：节点有两个红色的子节点

    • 操作：颜色翻转
    • 反转所有与该节点接触的链接的颜色，相当于把 2-3 Tree 的中间节点往上推

留下评论

猜您还喜欢