数据结构——堆和优先级队列

详细介绍见 Josh Hug 为 Berkeley CS61B 编写的教材

最新版本

一个数据结构可视化网站

Priority Queues

二叉搜索允许我们有效地进行快速搜索树，但如果我们更关心如何快速找到最小或是最大的元素呢？下面先给出最小优先级队列 Priority Queue 的 Abstract 数据类型：

/** (Min) Priority Queue: Allowing tracking and removal of
 * the smallest item in a priority queue. */
public interface MinPQ<Item> {
    /** Adds the item to the priority queue. */
    public void add(Item x);
    /** Returns the smallest item in the priority queue. */
    public Item getSmallest();
    /** Removes the smallest item from the priority queue. */
    public Item removeSmallest();
    /** Returns the size of the priority queue. */
    public int size();
}

Heaps

对于 PQ 操作，前面文章中所有数据结构中，用二叉搜索树实现是运行时间最佳的，但仍然可以进一步优化提升。我们规定 min-heap 的属性如下：

• Min-heap：每个节点都小于或等于其两个子节点；
• Complete：仅在底层缺少（若有），所有节点尽可能靠左。

例如上图中绿色的堆是有效的，红色的则是无效的

Tree Representation

• 方法一

  • Tree1A 固定节点宽度

    public class Tree1A<Key> {
      Key k;
      Tree1A left;
      Tree1A middle;
      Tree1A right;
    }
    

    可视化如下：

    

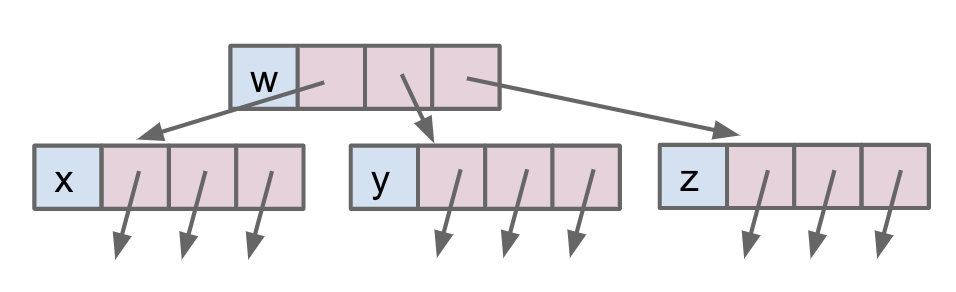
  • Tree1B 可变节点宽度

    public class Tree1B<Key> {
      Key k;
      Tree1B children;
    }
    

    可视化如下：

    

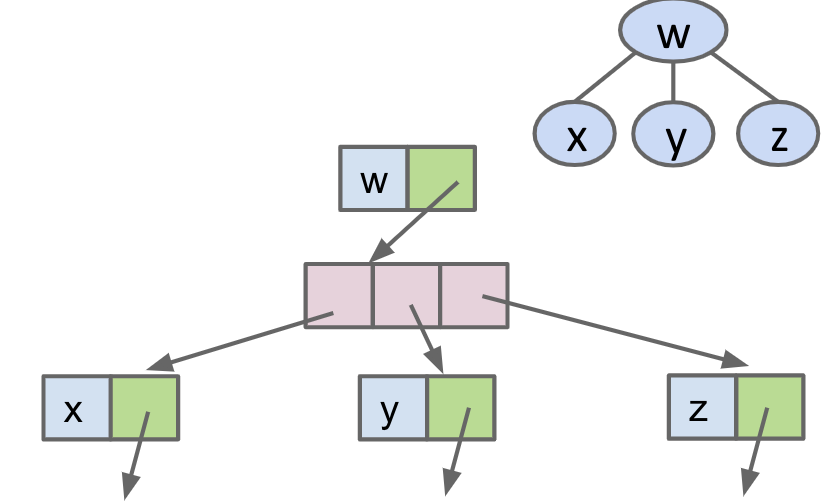
  • Tree1C 同级树

    public class Tree1C<Key> {
      Key k;
      Tree1C favoredChild;
      Tree1C sibling;
    }
    

    可视化如下：

    

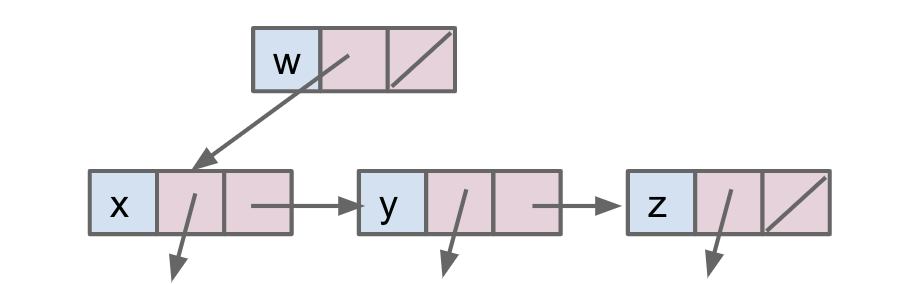
• 方法二

  重新调用不相交集的抽象数据结构，我们用数组来表示这个 Weighed Quick Union 结构

  public class Tree2<Key> {
    Key[] keys;
    int[] parents;
  }
  

  keys 数组表示索引映射到的键值，parents 数组表示该节点的父节点

  

  这样看 parents 数组似乎是冗余的，keys 中的顺序跟树的级别顺序安全相同。

• 方法三

  这种方法中，我们假设树是完整的，接着方法二中的发现，我们只用 keys 数组即可。

  public class Tree3<Key> {
    Key[] keys;
  }